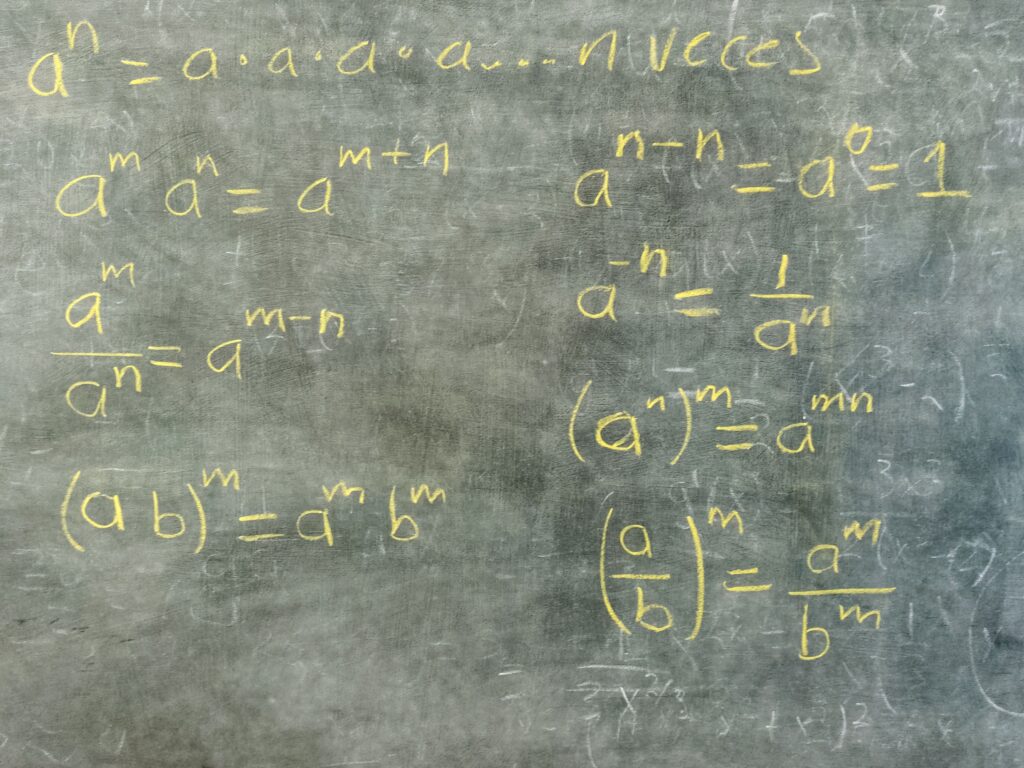Leyes de los exponentes.
Los exponentes son, una forma de notación para simplificar los cálculos ya que permite expresar productos de cantidades. Además es importante conocer las leyes que permiten manipular expresiones que tienen exponentes.
Tabla de contenidos.
Potencia de un número.
Primera ley de los exponentes
Tercera ley de los exponentes
Cuarta ley de los exponentes
Quinta ley de los exponentes
Exponentes negativos y ceros
Potencia de un número.
Cuando se efectúan multiplicaciones de mismo factor que se repiten 2,3,4 o más veces, se puede expresar de la siguiente forma:
a\cdot a
a \cdot a \cdot a
Pero imagina que el factor se debe multiplicar, digamos 10 veces o más sería muy difícil hacer operaciones usando esta notación.
Por eso se usa la notación exponencial, que es una forma de notación abreviada.
Así tenemos que:
a \cdot a = a^2
Se la anterior se lee: “a cuadrada”
a \cdot a \cdot a = a^3
La anterior se lee: “a cúbica”
a \cdot a \cdot a \cdot a = a^4
Esta última se lee: “a cuarta”
Entonces de forma general, el exponente de una expresión denota cuantas veces se está multiplicando.
a^n =a \cdot a \cdot a \cdot a \cdot a \cdot a .... n veces
Si a, es cualquier número y n es un entero positivo.
Al número a se le llama base y el número n es el exponente y muestra cuantas veces, será multiplicada la base por sí misma.
Se dice que n es la enésima potencia o el exponente; representa cuantas veces se está multiplicando el número llamado base.
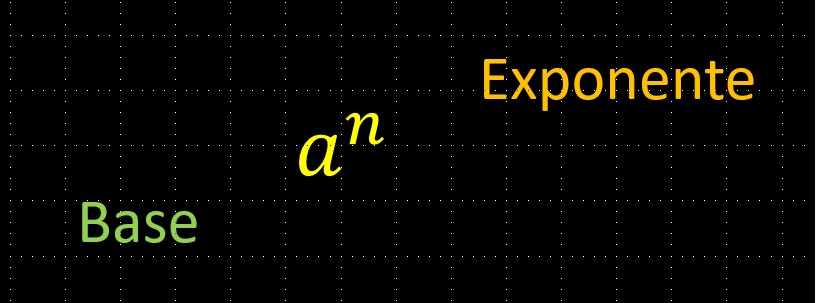
Ejemplo.
2^2 = 2 \cdot2 = 4
2^3 = 2 \cdot 2 \cdot 2 = 8

Primera ley de los exponentes.
Multiplicación de dos factores con la misma base y los exponentes pueden ser iguales o diferentes.
a^m a^n = a^{m+n}
a^2 a^3 = a a a a a a = a^5
En el ejemplo anterior el valor de m = 2 y n = 3, entonces m + n = 5
Ejemplos
a^4 a^3 = a^{4+3} = 2^7 b^3 b^2 b^5 = b^{3+2+5}= b^{10}2a^3b^2(3ab^4) = (2)(3)a^3 a^1 b^2 b^4 = 6 a^4 b^6 En este ejemplo se destaca que solo se suman los exponentes de los términos semejantes.
2b^2 ( a^2 + 3ab + 2b^2) = 2a^2b^2 + 6ab^3 + 4b^4Segunda ley de los exponentes.
\frac{a^m}{b^n} = a^{m-n}
m > n
\frac{a^m}{b^n} = 1
m = n
\frac{a^m}{b^n} = \frac{1}{a^{n-m}}
m < n
Tercera ley de los exponentes.
(a^m)^n=a^{mn}
Ejemplo
(a^2)^3=a^{6}
(aa)(aa)(aa)= a^6Cuarta ley de los exponentes.
(a b)^m=a^m b^m
Ejemplo
(a b)^3=(ab)(ab)(ab)=a^3 b^3