Inecuaciones de primer grado con una incógnita.

Tabla de contenidos.

Inecuación.

Una desigualdad con una o más cantidades desconocidas se llama inecuación. Las inecuaciones se llaman desigualdades condicionales. Una desigualdad condicional, es satisfecha por algunos, pero no por todos los valores permisibles de las variables correspondientes.

Ejemplo 1

La solución de la ecuación:

$2-3x \leq 2x+12$

La solución es:

$-2 \leq x$

Es decir que solo se cumple para valores mayores o iguales a -2, si en la ecuación (1) sustituimos x=2 entonces la inecuación queda:

$8 \leq 8$

Pero si sustituimos el valor x=-3 el resultado es:

$11 \leq 6$

Lo que es una contradicción, por esta razón es que son desigualdades condicionales pues los valores que las satisfacen, están limitados. Más adelante veremos como resolver estas inecuaciones.

Resolver inecuaciones.

Para resolver inecuaciones condicionales de debe encontrar los valores que la satisfacen, aplicando las propiedades de las desigualdades. También puedes ver el siguiente vídeo tutorial sobre este tema:

Propiedades de las desigualdades.

De forma general, las propiedades más destacadas son:

El sentido de la desigualdad no se altera al sumar o restar, la misma cantidad a ambos miembros.
Si ambos miembros de una desigualdad son multiplicados por el mismo número positivo no se altera el sentido de la desigualdad.
Cuando ambos miembros son multiplicados o divididos por un número negativo, si se invierte el sentido de la desigualdad.

Una desigualdad condicional, tiene un conjunto de soluciones que satisfacen la desigualdad, pero ese conjunto puede comenzar en un número en especial, antes de ese número o incluso el conjunto solución puede estar entre algúnos números, a esto se llama límite

Ejemplo 2

Obtener el conjunto solución o límite de la desigualdad:

$2-3x \leq 2x+12$

Debemos encontrar el valor de X para el cual es cierta la desigualdad, entonces despejamos esta variable: restando el número 12 a ambos lados de la desigualdad

$2-3x-12 \leq 2x+12-12$

$2-3x-12 \leq 2x$

Sumamos el -12 y 2 en el miembro izquierdo de la desigualdad:

$-3x-10 \leq 2x$

Ahora sumamos 3x a ambos miembros:

$-3x-10+3x \leq 2x +3x$

Hacemos operaciones, en el lado izquierdo se elimina 3x:

$-10 \leq 2x +3x$

Sumamos los términos semejantes del lado derecho:

$-10 \leq 5x$

Por último dividimos por 5 ambos miembros de la desigualdad:

$\frac{-10}{5} \leq \frac{5x}{5}$

Entonces:

$-2 \leq x$

El conjunto de soluciones para la desigualdad $2-3x \leq 2x+12$ es:

$S=\{x | -2 \leq x \}$

Como ya se mencionó en el ejemplo 1. solo puede tomar valores mayores o iguales-2 para que sea cierta.

Teoría de conjuntos

Interválos.

El conjunto de soluciones de una inecuación, se puede representar gráficamente en la recta real, además de su notación algebraica.

La solución para el ejemplo 2 fue $S=\{x | -2 \leq x \}$ , es decir los valores de x que pueden ser iguales a mayores que -2, es decir puede tomar el valor de 2 y cualquier valor mayor.

Gráficamente se representa en la recta real de la siguiente forma:

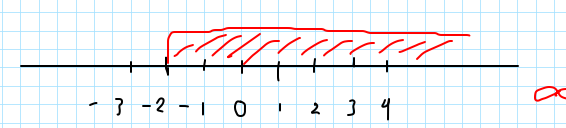
En la gráfica se representa que los valores pueden tomar desde el -2, incluyendo el -2 a partir de ahi cualquier valo que sea mayor.

En la siguiente imágen se agrega la notación algebraica y la notación gráfica que explíco a continuación:

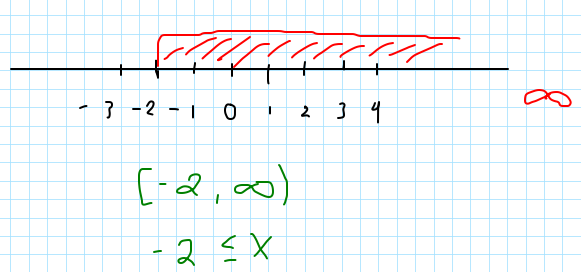
Los símbolos [ ] significan un interválo cerrado, lo que significa que el conjunto de soluciones puede tomar el valor que se indica, en este caso quiere decir que x puede tomar el valor de -2 y cualquier valor mayor $-2 \leq x$

Los parentésis se usan para indicar que el interválo es abierto, es decir que los vaores del conjunto solución no toman el valor indicado. así en la imagen anterior el intervalo es cerrado en -2 pues si toma el valor, pero por la derecha puede tomar cualquier número real por eso es abierto y se pone el signo de infinito.

Los interválos pueden ser cerrados, por ambos extremos, abiertos, cemicerrados o semi abiertos.

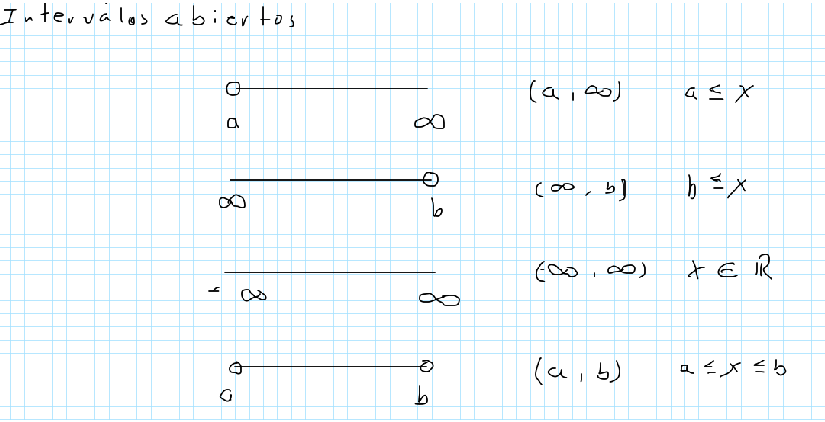
En la imagen anterior se muestran interválos abiertos.

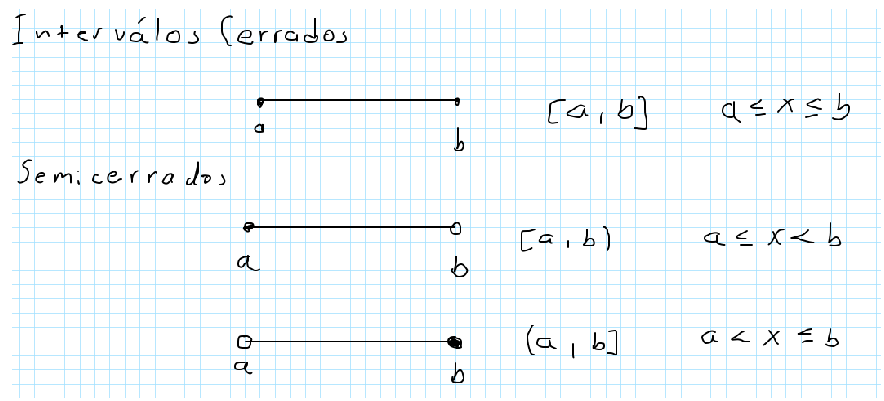
En esta imágen se muestra un interválo cerrado en la parte superior, en la parte media el interválo es cerrado por la izquierda y abierto por la derecha, es dceir tomara el valor de a, pero tomará todos los valores antes de b.

La parte inferior muestra un interválo abierto por la izquierda y cerrado por la derecha, entonces por el la izquierda toma los valores después de a, pero no a y por la derecha toma como máximo el valor de b.

Ejemplo 3

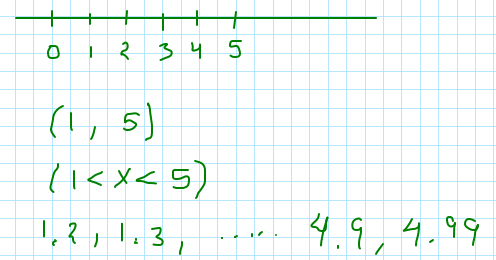
En la imágen anterior el interválo (1,5) toma los valores mayores a 1, pero no el 1, es decir 1.1, 1.2,1.3…4.90,4.91,4.92, y por la derecha toma todos los números reales antes de 5

Por favor dona cualquier cantidad para que este proyecto siga creciendo.