Gráficas de funciones (interpolación).
Tabla de contenidos.
- Plano cartesiano.
- Coordenadas Abcisa y ordenadas.
- Cuadrantes y signos.
- Ubicación de un punto por sus coordenadas.
- Grafica de una función.
- Breve estudio de Ecuaciones de primer grado
- Intercepciones con los ejes.
Plano cartesiano.
Los números reales se puede representar en la recta de los números reales, y tenemos una correspondencia entre cada número y un punto de la recta numérica.
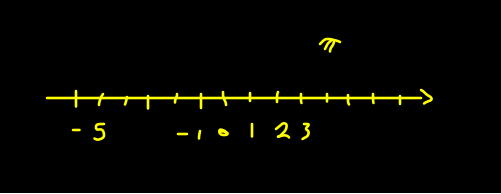
Si combinamos un par de rectas perpendiculares, donde ambas rectas representan número reales, entonces se forma un plano coordenado o plano de ejes coordenados rectángulares:
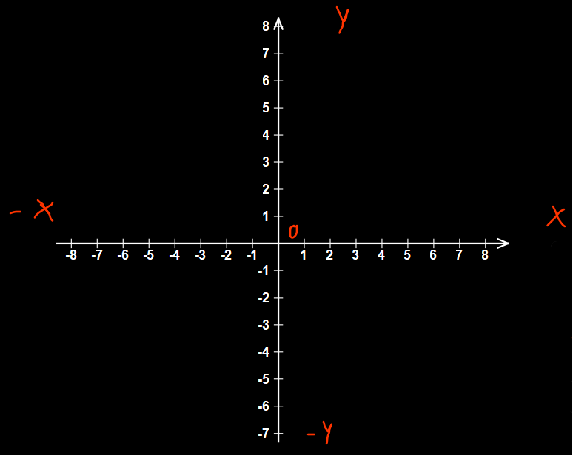
Figura 2 plano coordenado formado por dos rectas reales
El la figura 2 tenemos que se forma un plano por las rectas -XX e -YY que son perpendiculares. el punto donde se cruzan de llama origen O.
También se le conoce como plano cartesiano en honor a René Descartes.
Las dos rectas se llaman ejes coordenados el eje que se encuentra de forma horizontal -XX, se llama eje de las X o bien eje de las abscisas.
El eje perpendicular -YY se llama eje de las ordenadas. Este plano sirve para representar parejas de números formados por las funciones, es decir para prepresentar las relaciones entre dos variables.
En el eje de las abscisas los puntos a la derecha del punto O, llamado origen, representa valores positivos, los puntos a la izquierda representan valores negativos.
Para las ordenadas, los puntos arriba del origen, O, los valores son positivos, los valores debajo del punto de origen son negativos.
El plano coordenado o plano cartesiano es dividido en cuatro porciones que se llaman cuadrantes, los cuales se numeran en sentido contrario al de las manecillas del reloj:
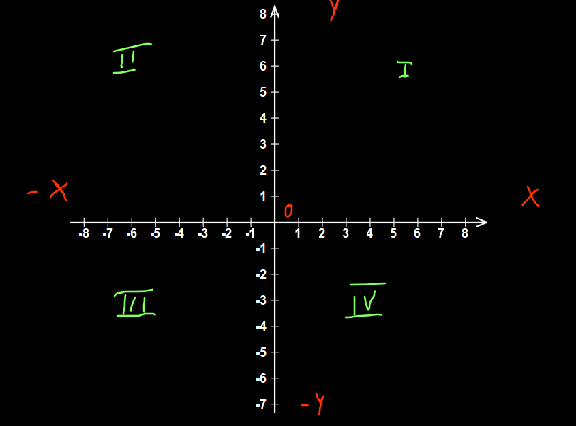
Figura 3 Cuadrantes en el plano coordenado.
Comenzando por la porción que se forma en la parte superior derecha de los cuatro cuadrantes, ese el el primer cuadrante y se continua numerando hacia la izquierda.
Coordenadas abscisa y ordenada.
Abscisa y ordenada, son los valores para poder localizar un punto en el plano cartesiano, señalando en donde se encuentra con respecto al origen, el origen es el punto de referencia para ubicar un punto.
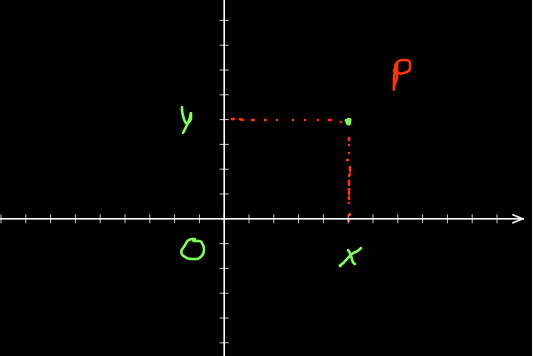
Figura 4 coordenadas abscisa y ordenada, indican la posición de un punto respecto a un plano.
Ubicar un punto en el plano, significa indicar cuales son sus coordenadas, es decir a que distancia de encuentra del origen y que que dirección. en este caso de la figura 4, para llegar al punto P desde el origen, primero debemos desplazarnos por el segmento \ \overrightarrow{OX}
Es decir desde el origen hay que desplazarse hacia la derecha hasta X.
Después hay que desplazarse desde X hacia arriba el segmento \ \overrightarrow{OY}
Las coordenadas funcionan commo cuando preguntas una direccción y la gente te dice “sigue en esta dirección 4 calles y después das vuelta a la izquierda, camina otras 3 calles y ahi esta…”
Cuadrantes y signos.
Ya mencionamos que hacia la derecha del eje de las abscisas es positivo y hacia arriba del del eje de las ordenadas, también los números son positivos.
Por lo que los signos de las coordenadas en cada cuadrante se conforman de la siguiente manera:
| Cuadrante | Signos Abscisa Ordenada |
| I | + + |
| II | – + |
| III | – – |
| IV | + – |
Ubicación de un punto por sus coordenadas.
Para ubicar un punto en el plano es precíso indicar el valor de las coordenadas del punto,en un par ordenado del tipo (X,Y).
La X es el valor de la abscisa, se coloca primero a la izquierda y representa el recorrido por el eje de las abscisas hacia el punto.
Y, representa el recorrido por el eje de las ordenadas hasta el punto.
Para ambas coordenadas, el signo nos va a indicar en que cuadrante se ubica el punto
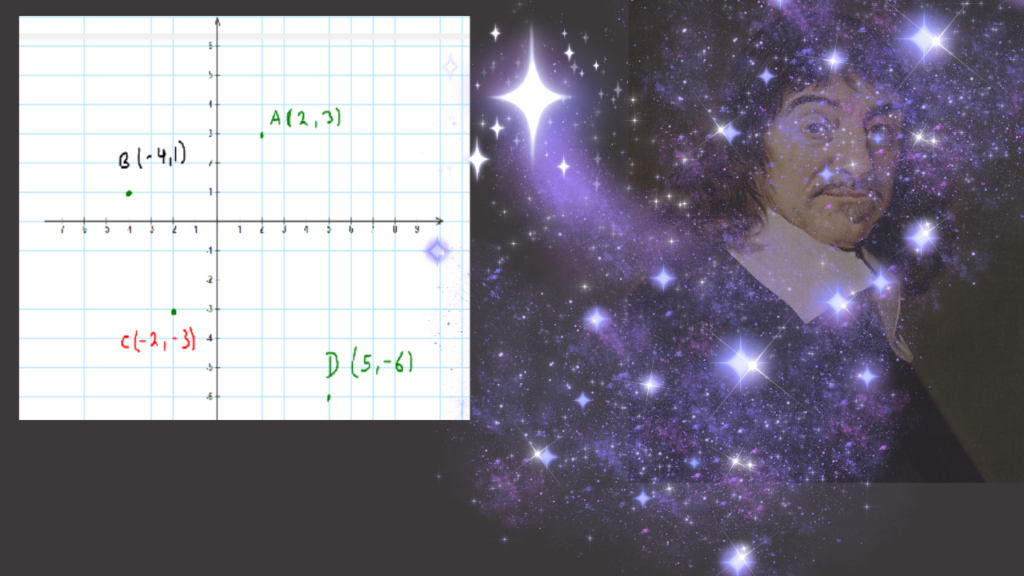
Ejemplo 1
Graficar los puntos.
- A(2,3)
- B(-4,1)
- C(-2,-3)
- D(5,-6)
Los puntos aparecen en la siguiente imagen:
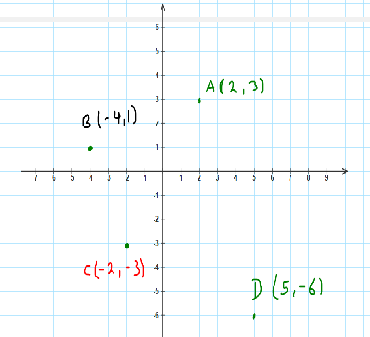
La ubicación del punto A es dos unidades a la derecha del origen sobre el eje de la abscisas, y 3 unidades hacia arriba respecto del eje de las ordenadas. Se encuentra en el primer cuadrante
El punto B(-4,1). se ubica 4 unidades a la izquierda sobre el eje de las ordenadas con respecto al origen porque el valor de la abscisa es -4, negativo. se encuentra en el segundo cuadrante
Punto C se encuentra en el tercer cuadrante, pues ambas coordenadas son negativas, asi se ubica a -2 unidades a la izquierda del origen, sobre las abscisas y -3 unidades hacia abajo del origen sobre las ordenadas.
Por último el punto D se ubica en el cuarto cuadrante, pues el valor de la abscisa es de 5 unidades positivas, por eso está a la derecha del origen. El valor de -6, para la ordenada lo ubica hacia abajo del origen.
Gráfica de una función. (interpolación)
Una función significa una relación de dependencia entre dos variables.
y=f(x)
Donde los valores de una variable depende de los valores que tome otra, por esta razón a la primera se le llama variable dependiente y a la segunda independiente. en la ecuación anterior x es la variable independiente, e y es la dependiente.
Por ejemplo en la ecuación y=3x
El valor de y depende del valor que se asigne a x:
Vamos a asignar algunos valores a x en la ecuación y=3x
si hacemos x=0 entonces y=3(0)
y=0Para x =1 tenemos y=3(1)
y=3Podemos construir una tabla con valores para x y calcular el valor de y:
Estos datos de pueden interpolar, es decir se forman las parejas de puntos de los conjuntos soluciones, que se pueden llevar a un plano cartesiano y graficar.
| Y | X |
| 0 | 0 |
| 3 | 1 |
| 6 | 2 |
| 9 | 3 |
Es decir se forman las parejas de puntos A(0,0), B(1,3), C(2,6), D(3,9). mismas que interpolamos en un plano cartesiano de la siguiente forma:
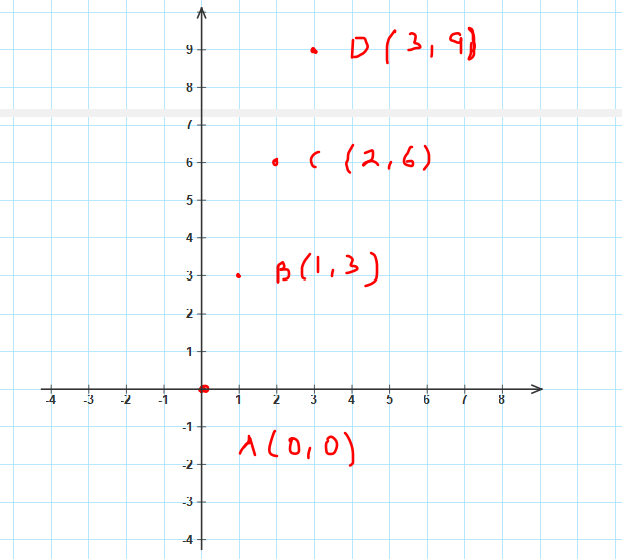
La interpolación o gráfica de los puntos de una función, permite estudiar como es la relación de una variable con respecto a otra, esto incluso nos permite hacer predicciones sobre el comportamiento de la variable dependiente y la independiente.
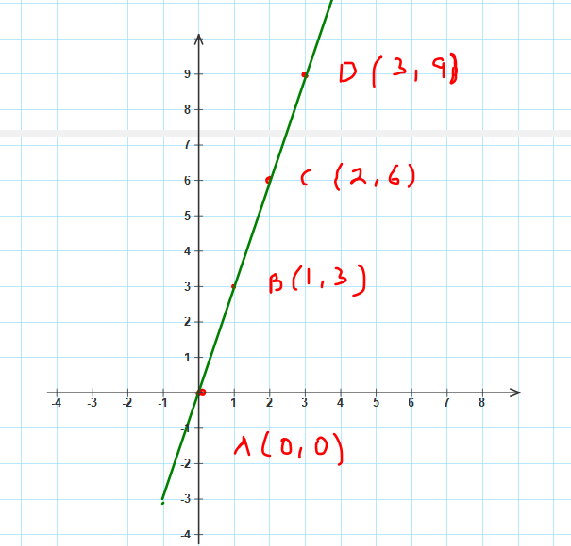
Finalmente se pueden unir los puntos por una línea y se ha de formar una recta.
Breve estudio de Ecuaciones de primer grado.
Todas las ecuaciones de primer grado cumplen con los siguientes principios:
- Las ecuaciones de primer grado representan una línea recta, por esta razón se llaman funciones líneales.
- Una ecuación del tipo y=ax donde a es una constante, es una función lineal que pasa por el origen.
- Si la ecuación tiene la forma y=ax+b, la ecuación no pasa por el origen, pero el valor de b es el valor del punto de intersección de la recta con el eje de las ordenadas. (0,b)
Ejemplo 1
Gráficar por el método de interpolación la ecuación: y=3x+2
Primero damos valores a x y los sustiruimos en y=3x+2 para obtener los valores de y y hacer la tabla de valores:
| Y | X |
| 2 | 0 |
| 5 | 1 |
| 8 | 2 |
| 11 | 3 |
Hacemos la interpolación:
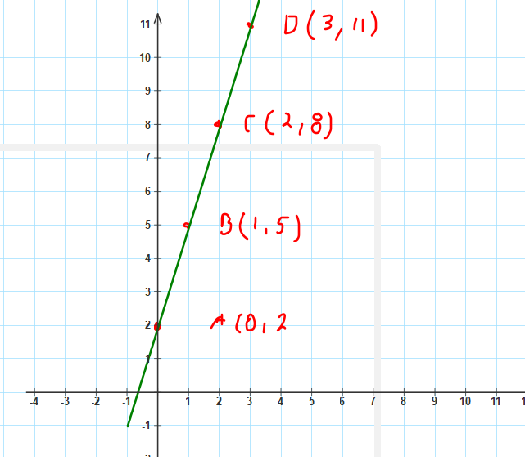
Gráfica de y=3x+2
Aqui podemos ver que b=2 es el punto de intersección con el eje de las ordenadas
Intercepciones con los ejes.
En la geometría elemental, sabemos que una recta puede quedar determinada por dos puntos, que pertenezcan a la misma.
En el caso de las ecuaciones líneales podemos obtener la gráfica de una recta, al determinar las intercepciones con los ejes; es decir los puntos donde la función lineal tiene contacto con los ejes coordenados.
Esto se logra igualando a 0 respectivamente las variables para en contrar la solución de la otra.
Ejemplo 2
Gráficar por el método de intercepciones
con los ejes la ecuación: y=3x+2
Primero hacemos x=0 para obtener el valor de y:
y=3(0)+2
y=2
Este valor es b que es el punto de intersección de y=3x+2 con el eje de las abscisas.
Ahora igualamos y=0 entonces 0=3x+2
despejando el valor de x
3x=-2
x=\frac{-2}{3} = -0.66
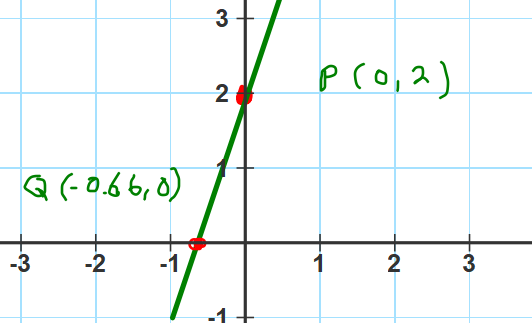
Puntos de inteersección con los ejes de y=3x+2
- Día internacional de las mujeres matemáticas
- Maryam Mirzajani
- Hipatia de Alejandria
- Numeros reales
- Euclides.
Dona cualquier cantidad o invítame un café para que el proyecto siga creciendo.